









We propose a novel point-based representation, Gaussian surfels, to combine the advantages of the flexible optimization procedure in 3D Gaussian points and the surface alignment property of surfels. This is achieved by directly setting the z-scale of 3D Gaussian points to 0, effectively flattening the original 3D ellipsoid into a 2D ellipse. Such a design provides clear guidance to the optimizer. By treating the local z-axis as the normal direction, it greatly improves optimization stability and surface alignment. While the derivatives to the local z-axis computed from the covariance matrix are zero in this setting, we design a self-supervised normal-depth consistency loss to remedy this issue. Monocular normal priors and foreground masks are incorporated to enhance the reconstruction quality, mitigating issues related to highlights and background. We propose a volumetric cutting method to aggregate the information of Gaussian surfels so as to remove erroneous points in depth maps generated by alpha blending. Finally, we apply screened Poisson reconstruction method to the fused depth maps to extract the surface mesh. Experimental results show that our method demonstrates superior performance in surface reconstruction compared to state-of-the-art neural volume rendering and point-based rendering methods.
Renderings & reconstructions on DTU, trained for ~6mins.
Renderings & reconstructions on BlendedMVS, trained for ~4mins.
Real-time rendering with high-quality underliying geometry.










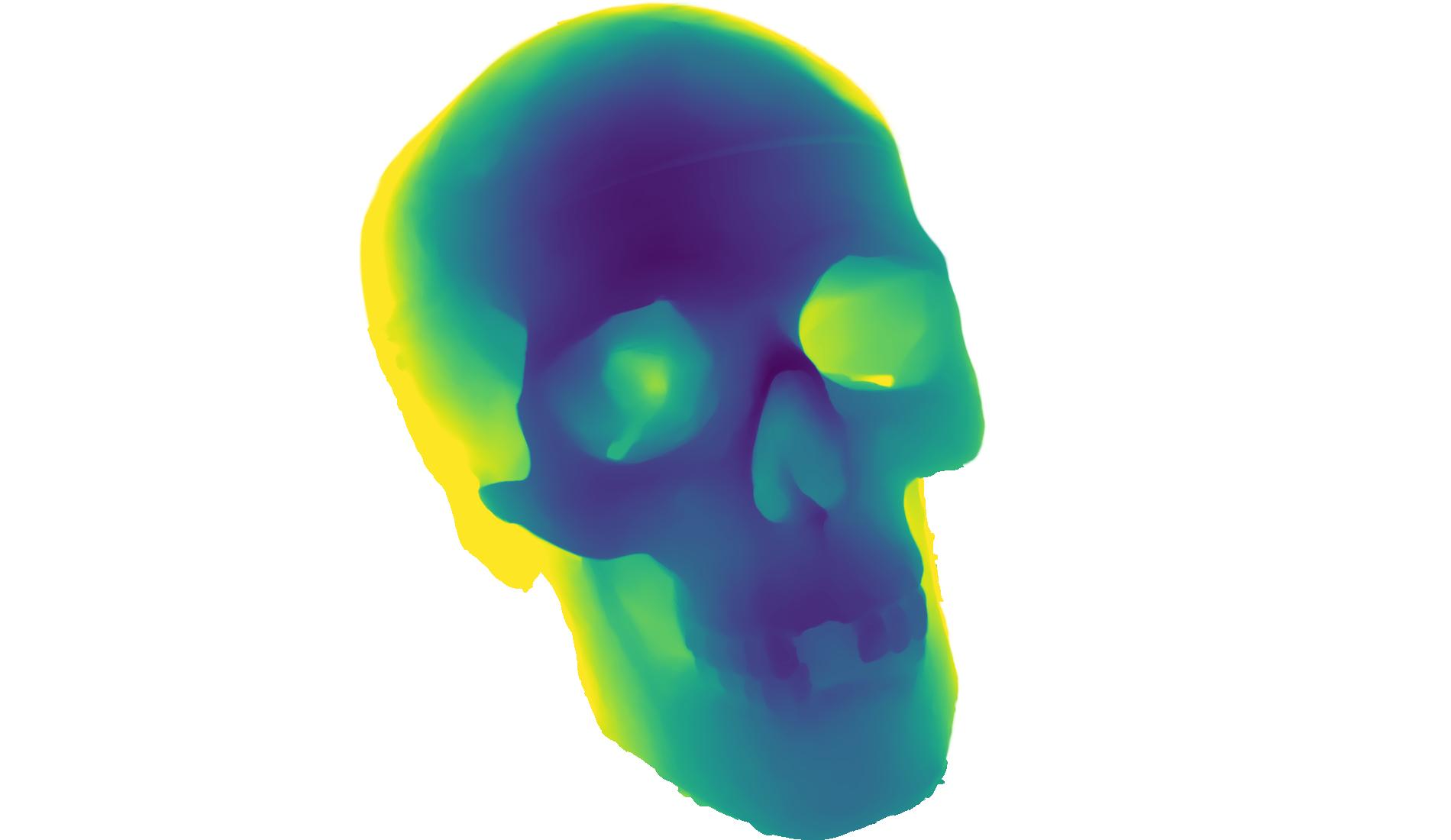


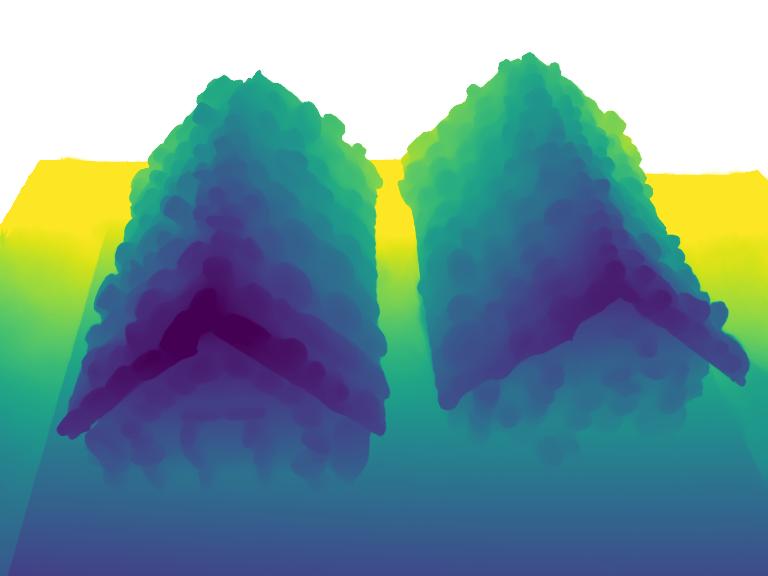





Learning progress of color, normal and depth from random initialization to 15k iterations in 5 minutes.
Comparing to SOTAs using Gaussian points and implicit SDF.














[Huang et al. 2024] 2DGS: 2D Gaussian Splatting for Geometrically Accurate Radiance Fields.
[Guédon et al. 2024] SuGaR: Surface-Aligned Gaussian Splatting for Efficient 3D Mesh Reconstruction and High-Quality Mesh Rendering.
[Kerbl et al. 2023] 3D Gaussian Splatting for Real-Time Radiance Field Rendering.
[Wang et al. 2023] NeuS2: Fast Learning of Neural Implicit Surfaces for Multi-view Reconstruction.
[Wang et al. 2021] NeuS: Learning Neural Implicit Surfaces by Volume Rendering for Multi-view Reconstruction.
[Yifan et al. 2019] Differentiable Surface Splatting for Point-based Geometry Processing.
[Zwicker et al. 2001] Surface Splatting.
[Pfister et al. 2000] Surfels: Surface Elements as Rendering Primitives.
@inproceedings{Dai2024GaussianSurfels,
author = {Dai, Pinxuan and Xu, Jiamin and Xie, Wenxiang and Liu, Xinguo and Wang, Huamin and Xu, Weiwei},
title = {High-quality Surface Reconstruction using Gaussian Surfels},
publisher = {Association for Computing Machinery},
booktitle = {ACM SIGGRAPH 2024 Conference Papers},
year = {2024},
articleno = {22},
numpages = {11}
}